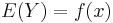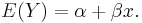Stimulus–response model
The stimulus–response model is a characterization of a statistical unit (such as a neuron) as a black box model, predicting a quantitative response to a quantitative stimulus, for example one administered by a researcher.
Fields of application
Stimulus–response models are applied in international relations,[1] psychology,[2] risk assessment,[3] neuroscience,[4] neurally-inspired system design,[5] and many other fields.
Mathematical formulation
The object of a stimulus–response model is to establish a mathematical function that describes the relation f between the stimulus x and the expected value (or other measure of location) of the response Y:
A common simplification assumed for such functions is linear, thus we expect to see a relationship like
Statistical theory for linear models has been well developed for more than fifty years, and a standard form of analysis called linear regression has been developed.
References
- ^ Greg Cashman (2000). "International Interaction: Stimulus–Response Theory and Arms Races". What causes war?: an introduction to theories of international conflict. Lexington Books. pp. 160–192. ISBN 9780739101124. http://books.google.com/books?id=I9xIfeijGhMC&pg=PA167&dq=stimulus-response-model+statistical#v=onepage&q=stimulus-response-model%20statistical&f=false.
- ^ Stephen P. Kachmar and Kimberly Blair (2007). "Counseling Across the Life Span". In Jocelyn Gregoire and Christin Jungers. The Counselor's Companion: What Every Beginning Counselor Needs to Know. Routledge. p. 143. ISBN 9780805856842. http://books.google.com/books?id=5V9nvsKeBgIC&pg=RA1-PA143&dq=stimulus-response-model++behavior#v=onepage&q=stimulus-response-model%20%20behavior&f=false.
- ^ Walter W. Piegorsch and A. John Bailer (2005). "Quantitative Risk Assessment with Stimulus–Response Data". Analyzing environmental data. John Wiley and Sons. pp. 171–214. ISBN 9780470848364. http://books.google.com/books?id=FrNv8AwkoKgC&pg=PA172&dq=stimulus-response-model+statistical#v=onepage&q=stimulus-response-model%20statistical&f=false.
- ^ Geoffrey W. Hoffmann (1988). "Neurons with hysteresis?". In Rodney Cotterill. Computer simulation in brain science. Cambridge University Press. pp. 74–87. ISBN 9780521341790. http://books.google.com/books?id=B6nfz--ePEEC&pg=PA79&dq=stimulus-response++neuron#v=onepage&q=stimulus-response%20%20neuron&f=false.
- ^ Teodor Rus (1993). Systems methodology for software. World Scientific. p. 12. ISBN 9789810212544. http://books.google.com/books?id=l7o31p-6dlAC&pg=PA12&dq=stimulus-response-model++neuron#v=onepage&q=stimulus-response-model%20%20neuron&f=false.